18. Astrology on the sphere (2)

                                                                                                                            Zawgyi version

စက္လံုးေပၚမွာ ေဗဒင္တြက္မလား (၂)

၂။ ေယာအတြင္းဝန္မင္း ဦးဘိုးလိႈင္၏ ေကာင္းကင္အယူအဆ။

ဥတုေဘာဇနသဂၤဟ က်မ္း၏ ၁။ ဥတုအရပ္ေဒသ ကိုျပျခင္း အခန္းတြင္ ေဖၚျပထားသည္မွာ  ………… ေနသြားလမ္း စြဲ၍ပူျခင္း ေအးျခင္း။ ေန၏ ေတာင္ေျမာက္ အယဥ္ႏွစ္ပါး၌ သြားျခင္းကို …………… ေကာင္းကင္၌ အေရွ႕ႏွင့္ အေနာက္ ေတာင္ႏွင့္ေျမာက္ မိုးကုပ္စက္၏ အဆံုးတိုင္ေအာင္ ဒယ္အိုးကင္းကို ေမွာက္၍ ထားသကဲ့သို႕ စက္ဝန္း၏ ထက္ဝက္ဟု စိတ္ကထင္မွတ္ၿပီးလွ်င္ စက္ ဝန္း အလံုးစံု၌ အံသာအားျဖင့္ သံုးရာ့ေျခာက္ဆယ္၊ တစ္အံသာလွ်င္ လိတၱာေျခာက္ဆယ္၊ အံသာ သံုးဆယ္လွ်င္ ရာသီတစ္ခု စိတ္ ကမွတ္၍ ထားၿပီးလွ်င္ ေနသည္ အလယ္မေဇၥ်လမ္းက ေတာင္သို႕ ႏွစ္ဆယ့္သံုးအံသာခြဲ ထြက္၍သြားၿပီးလွ်င္ ျပန္လာ၍၎၊ မေဇၥ် လမ္းမွ ေျမာက္သို႕ ႏွစ္ဆယ့္သံုးအံသာခြဲ ဝင္ျပန္၍ ေတာင္သို႕တဖန္ ထြက္သည္။ ဤသို႕ေနသည္ အနံအားျဖင့္ ေလးဆယ့္ခုနစ္အံ သာ အတြင္းတြင္ ေတာင္ေျမာက္ ဖယ္ရွား၍ လွည့္လည္၏။  …………  ဟုဆိုထားသည့္ အေလွ်ာက္ ေရွးအခါကပင္ ေကာင္းကင္ ကို စက္လံုးသ႑ာန္ တင္စား၍ ေန၊ လ၊ စသည္တို႕ ေရြ႕လ်ားရာလမ္းေၾကာင္း မ်ားအား စက္ဝိုင္းတို႕ျဖင့္ မွတ္သားၿပီး ယၡဳေခတ္အ ေခၚ စက္ဝန္း တစ္ခုကို ဒီဂရီ-၃၆ဝ၊ တစ္ဒီဂရီ ၁-ဒီဂရီ လွ်င္ ၆ဝ-မိနစ္၊ ၁-မိနစ္ လွ်င္ ၆ဝ-စကၠန္႕ စသည္္ျဖင့္ ပိုင္းျခား တိုင္းတာခဲ့ သည္မွာ အထင္အရွားပင္ ျဖစ္ပါသည္။

ယၡဳေခတ္တြင္ ဤကဲ့သို႕ လံုးဝန္းေသာ ဝတၱဳတစ္ခု အေပၚ၌တိုင္းတာ တြက္ခ်က္ေသာနည္း စံနစ္ကို စက္လံုးႀတိဂံသခ်ၤာနည္း (Spherical Trigonometry) ဟုေခၚဆိုသည္။ လံုးဝန္းေသာ ေကာင္းကင္စက္လံုးႏွင့္ ကမၻာေျမ စက္လံုးတို႕ေပၚ အေျခခံၿပီး အဆို ပါ စက္လံုးသခ်ၤာအားျဖင္ ့ရွင္းလင္းခ်က္မ်ား ဆြဲသားေဖၚျပရလွ်င္ နကၡတ္ေဗဒင္ပညာကို လ်င္ျမန္ လြယ္ကူစြာ သေဘာေပါက္ ေစ ႏိုင္မည္ ျဖစ္ပါသည္။

နကၡတၱေဗဒ ေလ့လာသူတို႕ အတြက္ေျမျပင္မွ ေကာင္းကင္သို႕ ေမာ္ၾကည့္လွ်င္ နကၡတ္တာရာ တို႕ကို အလြန္ႀကီးမားေသာစက္လံုး ျခမ္းႀကီးတစ္ခု၏ အတြင္း၌ ခ်ိတ္ဆြဲသြားလာ ေနသကဲ့သို႕ ထင္ရျမင္ရသည္။ မိုးကုတ္စက္ဝိုင္း ႀကီး၏ေအာက္ဖက္၌ ရွိသည့္ ၾကည့္ သူတို႕မျမင္ႏိုင္သည့္ အပိုင္းတြင္လည္း အလားတူ နကၡတ္တာရာ တို႕ျဖင့္ၿပီးသည့္ စက္လံုးျခမ္းႀကီးတစ္ခု ရွိေနဦးမည္ ဟူ၍လည္း ေတြးေတာၾကံဆ ၾကည့္ႏိုင္ပါသည္။ ထိုစက္လံုးျခမ္းႀကီး ႏွစ္ခုကို ဆက္စပ္ျခင္းအားၿဖင့္ ကမၻာေပၚမွ ၾကည့္သူတစ္ဦးအတြက္ မိမိ သည္ အလြန္ႀကီးမားသည့္ စက္လံုးႀကီးတစ္ခု၏ ဗဟိုခ်က္မွ ေကာင္းကင္သို႕ၾကည့္ရႈေနသည္ဟု ခံစားသိရွိႏိုင္သည္။ ထို႕ေၾကာင့္ နကၡတၱေဗဒ ေလ့လာမႈမ်ားကို ျပဳလုပ္ရာတြင္ ေကာင္းကင္စက္လံုး (Celestial sphere) တစ္ခုအၿဖစ္ စိတ္ကူးျဖင့္ ဖန္တီးလွ်က္ေန၊ လ ႏွင့္ နကၡတ္တာရာတို႕၏ တည္ေနရာ၊ လႈပ္ရွားသြားလာပံု အစရွိသည္တို႕အား မွတ္သားတြက္ယူေသာ အစဥ္အလာတစ္ရပ္ျဖစ္ ေပၚလာခဲ့သည္။

အမွန္အားျဖင့္ ေကာင္းကင္စက္လံုး၏ ဗဟိုခ်က္ရွိ မိမိတို႕ ရပ္တည္လ်က္ရွိေသာ ကမၻာသည္ပင္လွ်င္ စက္လံုးတခု အျဖစ္ယူဆႏိုင္ ျပန္သည္။ အဆိုပါ စက္လံုးသည္ ေကာင္းကင္စက္လံုးျဖင့္ ႏိႈင္းယွဥ္လွ်င္ အရြယ္အားျဖင့္ အလြန္ေသးငယ္သည္ကို ေတြ႕ႏိုင္ပါ သည္။ ကမၻာေပၚရွိ တိုင္းျပည္ အသီးသီးတို႕၏ တည္ေနရာမ်ား၊ ေန႕ႏွင့္ ညဥ့္တို႕ကို ျဖစ္ေစတတ္ေသာ ကမၻာ၏ လည္ပတ္မႈမ်ား စသည္တို႕အား တိုင္းတာရန္ ေျမျပင္စက္လံုး (Terrestial sphere) ဟူေသာ တိုင္းတာေရး စံနစ္တခုကို ဖန္တီး သံုးစြဲေလ့ရွိၾက သည္။ ဤအခန္းတြင္ စက္လံုးေပၚ၌ အေျခခံ၍ တိုင္းတာေသာနည္း စံနစ္ကို ေဆြးေႏြးတင္ျပၿပီး ထိုမွတဆင့္ ေရွ႕အခန္းမ်ားတြင္ ေျမျပင္စက္လံုး၊ ေကာင္းကင္စက္လံုး တို႕ေပၚ၌ အေသးစိတ္ တိုင္းတာပံုကို ဆက္လက္၍ ရွင္းလင္းလ်က္ စက္လံုးႏွစ္ခု၏ ဆက္စပ္ ရာမွ ကာလသံုးပါး၏ ျဖစ္စဥ္တို႕အား ေဟာေျပာႏိုင္သည့္ ဇာတာခြင္ ျဖစ္ေပၚလာပံုကိုလည္း တင္ျပသြားပါမည္။

၃။ စက္လံုး ဆိုသည္မွာ (What the sphere is)။

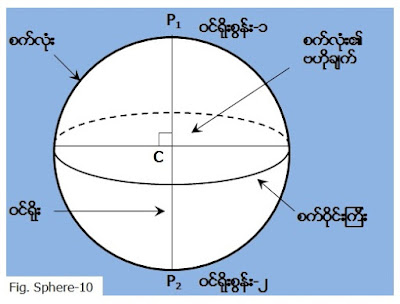
စက္လံုးဆိုသည္မွာ Fig. Sphere-8  တြင္ ျပထားသည့္ အတိုင္း ဗဟိုခ်က္တစ္ခု ျဖစ္ေသာ C မွတူညီသည့္ အခ်င္းဝက္ အကြာအ ေဝး R ရွိေသာ မ်က္နွာျပင္ခံုးတစ္ခု ၿဖစ္ပါသည္။ စက္လံုးေပၚ၌ ရွိေသာအမွတ္တစ္ခု P₁ မွ ဗဟိုခ်က္ C ကိုျဖတ္၍ ဆြဲသည့္ မ်ဥ္း ေျဖာင့္ တစ္ခုသည္ စက္လံုး၏ အျခားတစ္ဖက္ျခမ္း၌ ရွိေသာ အမွတ္တစ္ခု P₂ ကို Fig. Sphere-9 တြင္ျပထား သကဲ့သို႕ ျဖတ္ လ်ွက္ရွိေသာ မ်ဥ္းျဖစ္သည့္ P₁P₂ အား ဝင္ရိုး (Axis) ဟုေခၚသည္။  

 

ဝင္ရိုးအား ေထာင့္မတ္က်ေသာ ျပင္ညီမ်ားသည္ စက္လံုး၏ မ်က္ႏွာျပင္ကို စက္ဝိုင္း ျဖတ္ပိုင္းပံုမ်ားအျဖစ္ ပိုင္းျဖတ္ၾကသည္။ ထိုေထာင့္မတ္က်ေသာ ျပင္ညီသည္ ဗဟိုခ်က္ C ကိုျဖတ္လွ်င္  Fig. Sphere-10  တြင္ျပ ထားသကဲ့သို႕ စက္ဝိုင္းႀကီး (Great circle) တစ္ခုကို ျဖစ္ေစသည္။ စက္ဝိုင္းႀကီးသည္ စက္လံုးကို ႏွစ္ပိုင္း အညီအမွ် ပိုင္းျခားသည္။ အကယ္၍ ဗဟိုခ်က္ မဟုတ္သည့္ အျခားေသာ အမွတ္တစ္ခု ခု X ကို ျဖတ္ေသာ္ Fig. Sphere-11 တြင္ ျပထားသည့္အတိုင္း စက္ဝိုင္းေလး (Small circle) တစ္ခုကို ျဖစ္ေပၚေစသည္။ ဝင္ရိုးတစ္ ခုအတြက္ ပင္မစက္ဝိုင္းႀကီး တစ္ခုသာ ရွိႏိုင္ေသာ္လည္း X ၏အေနအထား ကိုလိုက္၍ စက္ဝိုင္းငယ္ မ်ားစြာရွိႏိုင္သည္။ စက္ဝိုင္းပံု တစ္ခုကို ေဘးဘက္မွ ေစာင္း၍ ၾကည့္ေသာ ျမင္ကြင္းတြင္ ဘဲဥပံုတစ္ခုကဲ့သို႕ျမင္ေတြ႕ရသည္။ ေဘး သို႕ေစာင္းေလေလ ျမင္ေတြ႕ရေသာ ဘဲဥပံုစံသည္ ျပားေလေလ ျဖစ္သည္။ ေဘးတိုက္ျမင္ရေသာ စက္ဝိုင္းမ်ားကို ဆြဲသားရာတြင္

ျမင္ႏိုင္ေသာ စက္ဝန္းပိုင္းကို မ်ဥ္းဆက္ျဖင့္ျပ၍ မျမင္ႏိုင္သည့္ စက္ဝန္းပိုင္းအား မ်ဥ္းျပတ္ျဖင့္ ျပေလ့ရွိသည္။ တခါတရံ မျမင္ႏိုင္ ေသာ စက္ဝန္းပိုင္းကို ခ်န္လွစ္၍ ျမင္ႏုိင္သည့္ စက္ဝန္းပိုင္းအား အနည္းငယ္ ဆက္ဆြဲျခင္း အားျဖင့္လည္း ျပသႏိုင္သည္။

ကမၻာ၏အီေကြတာ စက္ဝိုင္းႏွင့္ ေလာင္ဂ်ီတြဒ္ စက္ဝိုင္း အသီးသီးသည္ စက္ဝိုင္းႀကီးမ်ား ျဖစ္ၾက၍ အီေကြတာႏွင့္ ၿပိဳင္ၿပီး ေတာင္-ေျမာက္သို႕ မွတ္သားသည့္ လတၱီတြဒ္ စက္ဝိုင္းတို႕သည္ စက္ဝိုင္းေလးမ်ား ျဖစ္ၾကသည္။ မိုးကုတ္စက္ဝိုင္းႏွင့္ ေျမျပင္အထက္ရွိ ျမင္ႏိုင္ေသာ မြန္းတည့္စက္ဝိုင္း၊ ေျမျပင္ေအာက္ရွိ မျမင္ႏိုင္သည့္ သန္းေခါင္စက္ဝိုင္း တို႕သည္လည္း စက္ဝိုင္းႀကီးမ်ားပင္ ျဖစ္ၾကပါသည္။ အမွန္အားျဖင့္ မြန္းတည့္စက္ဝိုင္းႏွင့္ သန္းေခါင္စက္ဝိုင္း တို႕သည္ ဆက္လွ်က္တည္ရွိေသာ စက္ဝိုင္းႀကီး တစ္ခုတည္း ျဖစ္သည္။

စက္လံုး၏ ဝင္ရိုးတစ္ခုကို ေထာင့္မတ္က်ေသာ စက္ဝိုင္းႀကီးအား မူလစက္ဝိုင္း (Primary circle) ဟုေခၚ၍ ထိုစက္ဝိုင္းကို ေထာင့္ မတ္က်လွ်က္ ဝင္ရိုးအားျဖတ္သည့္ စက္ဝိုင္းႀကီး ေပါင္းမ်ားစြာ ဆြဲသားႏိုင္သည္။ Fig. Sphere-12 တြင္ျပထားသည့္ အဆိုပါ စက္ ဝိုင္း အမ်ိဳးအစားကို ထပ္ဆင့္စက္ဝိုင္း  (Seconday circle) ဟုေခၚသည္။ မူလစက္ဝိုင္း တစ္္ခုျဖစ္ေသာ ကမၻာ့အီေကြတာတြင္ ထပ္ဆင့္စက္ဝိုင္း ျဖစ္သည့္ ေလာင္ဂ်ီတြဒ္စက္ဝိုင္းေပါင္း မ်ားစြာရွိသည္။ မူလစက္ဝိုင္းႏွင့္ ၿပိဳင္၍ ဝင္ရိုးကို ေထာင့္မတ္က်ေအာင္ ဆြဲသားေသာ စက္ဝိုင္းမ်ားသည္ ဗဟိုခ်က္အား မျဖတ္ေသာေၾကာင့္ Fig. Sphere-13 တြင္ျပထား သကဲ့သို႕ စက္ဝိုင္းေလးမ်ား ျဖစ္ၾကသည္။ မူလစက္ဝိုင္းႀကီးႏွင့္ ေဝးေလေလ စက္ဝိုင္းေလး၏အရြယ္ ငယ္ ေလေလ ျဖစ္သည္။

စက္လံုးေပၚတြင္ တြြက္ခ်က္မႈမ်ား ေဆာင္ရြက္ရာ၌ စက္ဝိုင္းႀကီး သံုးခုျဖတ္သန္းရာမွ ျဖစ္ေပၚလာေသာ စက္လံုးႀတိဂံ တစ္ခုကို ဖြဲ႕စည္းလွ်က္ မည္ကဲ့သို႕ တြက္ခ်က္ေျဖရွင္း ရမည္ကို ေရွ႕တင္မည့္ ပို႕စ္တြင္ ဆက္လက္တင္ျပ သြားပါမည္။

           
AyeWinKyaw Blogpost 18.pdf
                                  

ayewinkyaw@ymail.com,                                         SMS: 09 459 824 750

30-11-2016                                                                                       ဆက္ရန္

Updated on 12-08-2017

-----------------------------------------------------------------------------------------------------
Unicode version

စက်လုံးပေါ်မှာ ဗေဒင်တွက်မလား (၂)

၂။ ယောအတွင်းဝန်မင်း ဦးဘိုးလှိုင်၏ ကောင်းကင်အယူအဆ။

ဥတုဘောဇနသင်္ဂဟ ကျမ်း၏ ၁။ ဥတုအရပ်ဒေသ ကိုပြခြင်း အခန်းတွင် ဖေါ်ပြထားသည်မှာ  ………… နေသွားလမ်း စွဲ၍ပူခြင်း အေးခြင်း။ နေ၏ တောင်မြောက် အယဉ်နှစ်ပါး၌ သွားခြင်းကို …………… ကောင်းကင်၌ အရှေ့နှင့် အနောက် တောင်နှင့်မြောက် မိုးကုပ်စက်၏ အဆုံးတိုင်အောင် ဒယ်အိုးကင်းကို မှောက်၍ ထားသကဲ့သို့ စက်ဝန်း၏ ထက်ဝက်ဟု စိတ်ကထင်မှတ်ပြီးလျှင် စက် ဝန်း အလုံးစုံ၌ အံသာအားဖြင့် သုံးရာ့ခြောက်ဆယ်၊ တစ်အံသာလျှင် လိတ္တာခြောက်ဆယ်၊ အံသာ သုံးဆယ်လျှင် ရာသီတစ်ခု စိတ် ကမှတ်၍ ထားပြီးလျှင် နေသည် အလယ်မဇ္ဈေလမ်းက တောင်သို့ နှစ်ဆယ့်သုံးအံသာခွဲ ထွက်၍သွားပြီးလျှင် ပြန်လာ၍၎င်း၊ မဇ္ဈေ လမ်းမှ မြောက်သို့ နှစ်ဆယ့်သုံးအံသာခွဲ ဝင်ပြန်၍ တောင်သို့တဖန် ထွက်သည်။ ဤသို့နေသည် အနံအားဖြင့် လေးဆယ့်ခုနစ်အံ သာ အတွင်းတွင် တောင်မြောက် ဖယ်ရှား၍ လှည့်လည်၏။  …………  ဟုဆိုထားသည့် အလျှောက် ရှေးအခါကပင် ကောင်းကင် ကို စက်လုံးသဏ္ဍာန် တင်စား၍ နေ၊ လ၊ စသည်တို့ ရွေ့လျားရာလမ်းကြောင်း များအား စက်ဝိုင်းတို့ဖြင့် မှတ်သားပြီး ယ္ခုခေတ်အ ခေါ် စက်ဝန်း တစ်ခုကို ဒီဂရီ-၃၆ဝ၊ ၁-ဒီဂရီ လျှင် ၆ဝ-မိနစ်၊ ၁-မိနစ် လျှင် ၆ဝ-စက္ကန့် စသည်ဖြင့် ပိုင်းခြား တိုင်းတာခဲ့ သည်မှာ အထင်အရှားပင် ဖြစ်ပါသည်။

ယ္ခုခေတ်တွင် ဤကဲ့သို့ လုံးဝန်းသော ဝတ္တုတစ်ခု အပေါ်၌တိုင်းတာ တွက်ချက်သောနည်း စံနစ်ကို စက်လုံးတြိဂံသင်္ချာနည်း (Spherical Trigonometry) ဟုခေါ်ဆိုသည်။ လုံးဝန်းသော ကောင်းကင်စက်လုံးနှင့် ကမ္ဘာမြေ စက်လုံးတို့ပေါ် အခြေခံပြီး အဆို ပါ စက်လုံးသင်္ချာအားဖြင် ရှင်းလင်းချက်များ ဆွဲသားဖေါ်ပြရလျှင် နက္ခတ်ဗေဒင်ပညာကို လျင်မြန် လွယ်ကူစွာ သဘောပေါက် စေ နိုင်မည် ဖြစ်ပါသည်။

နက္ခတ္တဗေဒ လေ့လာသူတို့ အတွက်မြေပြင်မှ ကောင်းကင်သို့ မော်ကြည့်လျှင် နက္ခတ်တာရာ တို့ကို အလွန်ကြီးမားသောစက်လုံး ခြမ်းကြီးတစ်ခု၏ အတွင်း၌ ချိတ်ဆွဲသွားလာ နေသကဲ့သို့ ထင်ရမြင်ရသည်။ မိုးကုတ်စက်ဝိုင်း ကြီး၏အောက်ဖက်၌ ရှိသည့် ကြည့် သူတို့မမြင်နိုင်သည့် အပိုင်းတွင်လည်း အလားတူ နက္ခတ်တာရာ တို့ဖြင့်ပြီးသည့် စက်လုံးခြမ်းကြီးတစ်ခု ရှိနေဦးမည် ဟူ၍လည်း တွေးတောကြံဆ ကြည့်နိုင်ပါသည်။ ထိုစက်လုံးခြမ်းကြီး နှစ်ခုကို ဆက်စပ်ခြင်းအားဖြင့် ကမ္ဘာပေါ်မှ ကြည့်သူတစ်ဦးအတွက် မိမိ သည် အလွန်ကြီးမားသည့် စက်လုံးကြီးတစ်ခု၏ ဗဟိုချက်မှ ကောင်းကင်သို့ကြည့်ရှုနေသည်ဟု ခံစားသိရှိနိုင်သည်။ ထို့ကြောင့် နက္ခတ္တဗေဒ လေ့လာမှုများကို ပြုလုပ်ရာတွင် ကောင်းကင်စက်လုံး (Celestial sphere) တစ်ခုအဖြစ် စိတ်ကူးဖြင့် ဖန်တီးလျှက်နေ၊ လ နှင့် နက္ခတ်တာရာတို့၏ တည်နေရာ၊ လှုပ်ရှားသွားလာပုံ အစရှိသည်တို့အား မှတ်သားတွက်ယူသော အစဉ်အလာတစ်ရပ်ဖြစ် ပေါ်လာခဲ့သည်။

အမှန်အားဖြင့် ကောင်းကင်စက်လုံး၏ ဗဟိုချက်ရှိ မိမိတို့ ရပ်တည်လျက်ရှိသော ကမ္ဘာသည်ပင်လျှင် စက်လုံးတခု အဖြစ်ယူဆနိုင် ပြန်သည်။ အဆိုပါ စက်လုံးသည် ကောင်းကင်စက်လုံးဖြင့် နှိုင်းယှဉ်လျှင် အရွယ်အားဖြင့် အလွန်သေးငယ်သည်ကို တွေ့နိုင်ပါ သည်။ ကမ္ဘာပေါ်ရှိ တိုင်းပြည် အသီးသီးတို့၏ တည်နေရာများ၊ နေ့နှင့် ညဉ့်တို့ကို ဖြစ်စေတတ်သော ကမ္ဘာ၏ လည်ပတ်မှုများ စသည်တို့အား တိုင်းတာရန် မြေပြင်စက်လုံး (Terrestial sphere) ဟူသော တိုင်းတာရေး စံနစ်တခုကို ဖန်တီး သုံးစွဲလေ့ရှိကြ သည်။ ဤအခန်းတွင် စက်လုံးပေါ်၌ အခြေခံ၍ တိုင်းတာသောနည်း စံနစ်ကို ဆွေးနွေးတင်ပြပြီး ထိုမှတဆင့် ရှေ့အခန်းများတွင် မြေပြင်စက်လုံး၊ ကောင်းကင်စက်လုံး တို့ပေါ်၌ အသေးစိတ် တိုင်းတာပုံကို ဆက်လက်၍ ရှင်းလင်းလျက် စက်လုံးနှစ်ခု၏ ဆက်စပ် ရာမှ ကာလသုံးပါး၏ ဖြစ်စဉ်တို့အား ဟောပြောနိုင်သည့် ဇာတာခွင် ဖြစ်ပေါ်လာပုံကိုလည်း တင်ပြသွားပါမည်။

၃။ စက်လုံး ဆိုသည်မှာ (What the sphere is)။

စက်လုံးဆိုသည်မှာ Fig. Sphere-8  တွင် ပြထားသည့် အတိုင်း ဗဟိုချက်တစ်ခု ဖြစ်သော C မှတူညီသည့် အချင်းဝက် အကွာအ ဝေး R ရှိသော မျက်နှာပြင်ခုံးတစ်ခု ဖြစ်ပါသည်။ စက်လုံးပေါ်၌ ရှိသောအမှတ်တစ်ခု P₁ မှ ဗဟိုချက် C ကိုဖြတ်၍ ဆွဲသည့် မျဉ်း ဖြောင့် တစ်ခုသည် စက်လုံး၏ အခြားတစ်ဖက်ခြမ်း၌ ရှိသော အမှတ်တစ်ခု P₂ ကို Fig. Sphere-9 တွင်ပြထား သကဲ့သို့ ဖြတ် လျှက်ရှိသော မျဉ်းဖြစ်သည့် P₁P₂ အား ဝင်ရိုး (Axis) ဟုခေါ်သည်။

ဝင်ရိုးအား ထောင့်မတ်ကျသော ပြင်ညီများသည် စက်လုံး၏ မျက်နှာပြင်ကို စက်ဝိုင်း ဖြတ်ပိုင်းပုံများအဖြစ် ပိုင်းဖြတ်ကြသည်။ ထိုထောင့်မတ်ကျသော ပြင်ညီသည် ဗဟိုချက် C ကိုဖြတ်လျှင်  Fig. Sphere-10  တွင်ပြ ထားသကဲ့သို့ စက်ဝိုင်းကြီး (Great circle) တစ်ခုကို ဖြစ်စေသည်။ စက်ဝိုင်းကြီးသည် စက်လုံးကို နှစ်ပိုင်း အညီအမျှ ပိုင်းခြားသည်။ အကယ်၍ ဗဟိုချက် မဟုတ်သည့် အခြားသော အမှတ်တစ်ခု ခု X ကို ဖြတ်သော် Fig. Sphere-11 တွင် ပြထားသည့်အတိုင်း စက်ဝိုင်းလေး (Small circle) တစ်ခုကို ဖြစ်ပေါ်စေသည်။ ဝင်ရိုးတစ်ခုအတွက် ပင်မစက်ဝိုင်းကြီး တစ်ခုသာ ရှိနိုင်သော်လည်း X ၏အနေအထား ကိုလိုက်၍ စက်ဝိုင်းငယ် များစွာရှိနိုင်သည်။ စက်ဝိုင်းပုံ တစ်ခုကို ဘေးဘက်မှ စောင်း၍ ကြည့်သော မြင်ကွင်းတွင် ဘဲဥပုံတစ်ခုကဲ့သို့မြင်တွေ့ရသည်။ ဘေး သို့စောင်းလေလေ မြင်တွေ့ရသော ဘဲဥပုံစံသည် ပြားလေလေ ဖြစ်သည်။ ဘေးတိုက်မြင်ရသော စက်ဝိုင်းများကို ဆွဲသားရာတွင်မြင် နိုင်သော စက်ဝန်းပိုင်းကို မျဉ်းဆက်ဖြင့်ပြ၍ မမြင်နိုင်သည့် စက်ဝန်းပိုင်းအား မျဉ်းပြတ်ဖြင့် ပြလေ့ရှိသည်။ တခါတရံ မမြင်နိုင် သော စက်ဝန်းပိုင်းကို ချန်လှစ်၍ မြင်နိုင်သည့် စက်ဝန်းပိုင်းအား အနည်းငယ် ဆက်ဆွဲခြင်း အားဖြင့်လည်း ပြသနိုင်သည်

ကမ္ဘာ၏အီကွေတာ စက်ဝိုင်းနှင့် လောင်ဂျီတွဒ် စက်ဝိုင်း အသီးသီးသည် စက်ဝိုင်းကြီးများ ဖြစ်ကြ၍ အီကွေတာနှင့် ပြိုင်ပြီး တောင်-မြောက်သို့ မှတ်သားသည့် လတ္တီတွဒ် စက်ဝိုင်းတို့သည် စက်ဝိုင်းလေးများ ဖြစ်ကြသည်။ မိုးကုတ်စက်ဝိုင်းနှင့် မြေပြင်အထက်ရှိ မြင် နိုင်သော မွန်းတည့်စက်ဝိုင်း၊ မြေပြင်အောက်ရှိ မမြင်နိုင်သည့် သန်းခေါင်စက်ဝိုင်း တို့သည်လည်း စက်ဝိုင်းကြီးများပင် ဖြစ်ကြပါ သည်။ အမှန်အားဖြင့် မွန်းတည့်စက်ဝိုင်းနှင့် သန်းခေါင်စက်ဝိုင်း တို့သည် ဆက်လျှက်တည်ရှိသော စက်ဝိုင်းကြီး တစ်ခုတည်း ဖြစ် သည်။

စက်လုံး၏ ဝင်ရိုးတစ်ခုကို ထောင့်မတ်ကျသော စက်ဝိုင်းကြီးအား မူလစက်ဝိုင်း (Primary circle) ဟုခေါ်၍ ထိုစက်ဝိုင်းကို ထောင့် မတ်ကျလျှက် ဝင်ရိုးအားဖြတ်သည့် စက်ဝိုင်းကြီး ပေါင်းများစွာ ဆွဲသားနိုင်သည်။ Fig. Sphere-12 တွင်ပြထားသည့် အဆိုပါ စက် ဝိုင်း အမျိုးအစားကို ထပ်ဆင့်စက်ဝိုင်း  (Seconday circle) ဟုခေါ်သည်။ မူလစက်ဝိုင်း တစ်ခုဖြစ်သော ကမ္ဘာ့အီကွေတာတွင် ထပ် ဆင့်စက်ဝိုင်း ဖြစ်သည့် လောင်ဂျီတွဒ်စက်ဝိုင်းပေါင်း များစွာရှိသည်။ မူလစက်ဝိုင်းနှင့် ပြိုင်၍ ဝင်ရိုးကို ထောင့်မတ်ကျအောင် ဆွဲသား သော စက်ဝိုင်းများသည် ဗဟိုချက်အား မဖြတ်သောကြောင့် Fig. Sphere-13 တွင်ပြထား သကဲ့သို့ စက်ဝိုင်းလေးများ ဖြစ်ကြသည်။ မူလစက်ဝိုင်းကြီးနှင့် ဝေးလေလေ စက်ဝိုင်းလေး၏အရွယ် ငယ် လေလေ ဖြစ်သည်။

စက်လုံးပေါ်တွင် တွက်ချက်မှုများ ဆောင်ရွက်ရာ၌ စက်ဝိုင်းကြီး သုံးခုဖြတ်သန်းရာမှ ဖြစ်ပေါ်လာသော စက်လုံးတြိဂံ တစ်ခုကို ဖွဲ့ စည်းလျှက် မည်ကဲ့သို့ တွက်ချက်ဖြေရှင်း ရမည်ကို ရှေ့တင်မည့် ပို့စ်တွင် ဆက်လက်တင်ပြ သွားပါမည်။

AyeWinKyaw Blogpost 18.pdf

ayewinkyaw@ymail.com,                          SMS: 09 459 824 750

30-11-2016                                                                 ဆက်ရန်